Dennis Reinhardt Dec. 31, 2023
Ionic visualization
Ionic: One-Shot Neural Network Learning
Overview
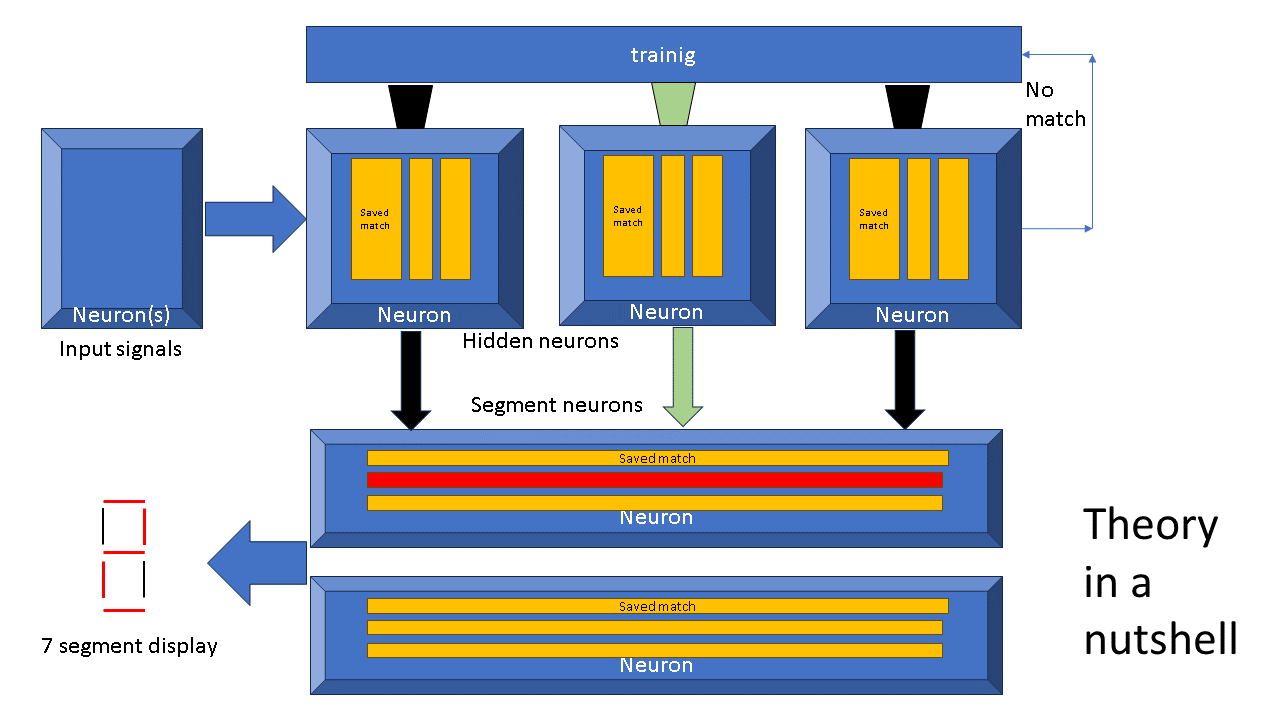
Fig. 1 Shows the architecture used to learn. The number of hidden neurons ranges from 0, direct connect of input to segments, to 16, 1 per decoded input. The network is feedforward and layered, with the exception of the no match signal fed back to the training network and used to instantiate a new stored match in a selected subset of the hidden neurons.
|
While trying to model the 7-segment learning problem, we discovered a quite different approach to solving this problem. A key advantage of this new model, called Ionic, is training can occur in a single supervised training pass or by accretion where new training sessions are laid down without invalidating previous training.
One of the key differences of Ionic and widely used back-prop network models is that Ionic memorizes the input-output connections. There are no weights. Each connection and its stored value is binary: 0 or 1.
When a vector set of inputs matches a stored vector match, that neuron it is stored in fires. Because short vector sets can be represented as bits within a single computer word, the decision to fire is can be implemented more efficiently than the comparable decision within a back-prop neuron: float-point multiply inputs by weights and add up the resulting partial product into a sum.
Training is triggered to commence when none of the hidden neurons has the input pattern stored. Consider the simplest case where each new match pattern is assigned to a new neuron. Each hidden neuron makes a connection to segments which need to be lit. The model is trained in one pass.
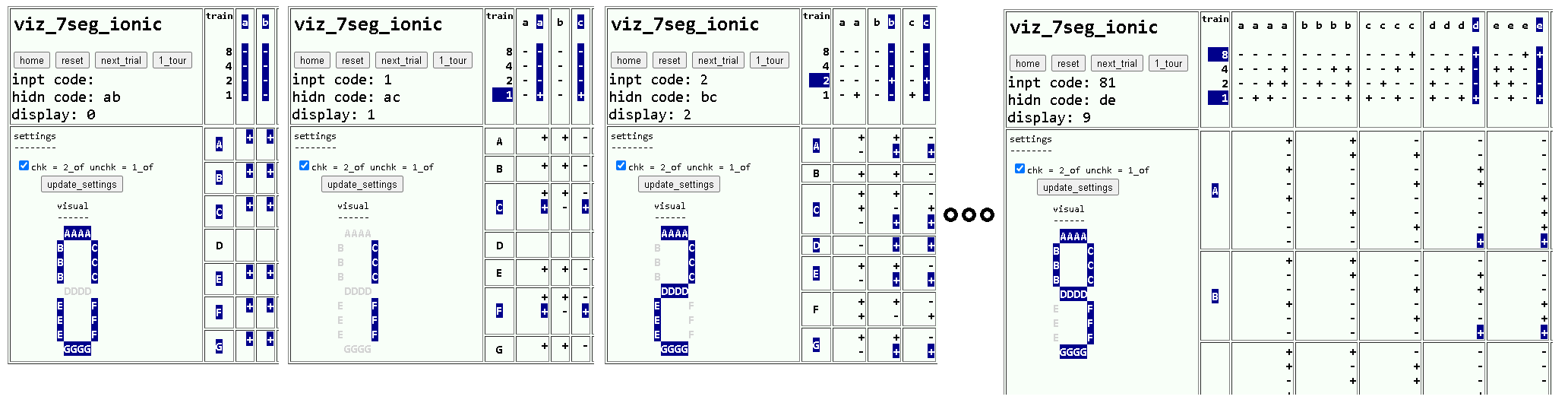
Illustrating 2_of hidden neuron coding
|
|
Fig. 2 Shown are 4 different training sessions. The leftmost shows the 8-4-2-1 input pattern of 0000 is saved in the a nd b hidden neurons as ----. The segment neurons below require both a nd b hidden neuron output before they connect up ABCEFG segments to light a visible "0". The input pattern of 0001 is stored in a different two columns a and c. By the time training reaches input 1001, all 10 digits have been learned without overwriting previous learning.
|
Fig. 2 illustrates a training progression for inputs 0000 through 1001, digits 0 through 9. Here is the assignment algorithm used in the training:
number columns selected
------ -------------------
0 a b
1 a c
2 b c
3 a d
4 b d
5 c d
6 e e
7 b e
8 c e
9 d e
We can recast and extend this to determine how many hidden neurons are required to represent a number of hidden states:
column added index running sum
------------ ----- -----------
a 0 0
b 1 1 = 0 + 1
c 2 3 = 1 + 2
d 3 6 = 3 + 3
e 4 10 = 6 + 4
f 5 15 = 10 + 5
...
We do not yet propose a specific mechanism to implement the training, leaving that to the future. It could require a different mechanism than the retained match used here in Ionic. Differing mechanisms should not be difficult to justify on biological plausibility. In humans, there are 3,300 types of brain cells [1][2]. So, even without an implementation, we can specify what the training does.
The training mechanism sends individual signals to each hidden neuron, telling the neuron to memorize the input. Should the number N of hidden neurons be at a capacity limit for 2_of_N, training is responsible for adding an Nth+1 neuron.
In a computer implementation, acquiring a new neuron is a common operation equivalent to a malloc (memory allocation) call in the program.
In a biological implentation, the combination of dynamic assignment and 2_of coding is attractive.
Dynamic assignment is an attractive way to add an Nth+1 neuron. Almost assuredly, that Nth+1 neuron already has other stimuli it responds to. So, if we relied on N+1 alone, a false match could be generated when previous, likely poorly related, stored matches. The 2_of coding reduces the likelihood of false matches, considerably. Using 3_of, 4_of, and so on coding can further drive down the production of false matches.
Dynamic assignment is attractive in a biological model.
Without 2_of (or higher) coding of the output of the hidden neurons, it is necessary to weave the new Nth+1 hidden neuron output into all the past connections. With such coding, we can just accrete new connections without having to augment any past connections with new terms.
Other work
The perceptron model has a long history in AI including 1943 invention by McCulloch and Pitts, description in 1958 by Rosenblatt, devastating critiqued in 1969 by Minsky and Papert, and resuscitated in 1986 by the Backpropagation algorithm by Rumelhart, Hinton, and Williams.
Backprop simply dominates AI neural net model learning. From the perspective of this huge intellectual legacy, Iocic model can be questioned on ability to generalize and how it handles inexact input. Finally, BackProp subsumes the Ionic model insofar as a match vector can be represented by an appropriate weighting vector.
Granted, Ionic is limited in application. It solves the 7-segment display problem amazingly well, in a single pass. Perhaps there are other problems it can solve. Publishing this admittedly preliminary description is one way to find out.
Finally, we should acknowledge our awareness of hyperdimensional computing [3]. They have a formal algebra built on binding, superposition, and shuffling. In Ionic, all of this relationship is reduced to match or no match on input.
Revision history
| Dec. 31, 2023 |
First publication |
| Dec. 28, 2023 |
Draft |
References and notes

